cisBlog
0%

初识全同态加密

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 3.2k 阅读时长 ≈ 3 分钟

近年来，隐私保护的话题越来越引起人们的重视，使得同态加密等一系列密码学应用技术得到广泛的普及。因此，我想对全同态加密（Fully Homomorphic Encryption，FHE）稍作介绍一下。

FHE的定义

FHE通俗来说就是一共有$n$个数$m_1, m_2, \ldots, m_n$，加密后对其进行某个函数运算$f(E(m_1), E(m_2), \ldots, E(m_n))$，解密后获得最终运算结果$D(f(E(m_1), E(m_2), \ldots, E(m_n)))$，在这个过程中不暴露$n$个数本身的数值。

  • 例如，4名员工在相互不知道薪水的情况下，计算他们的平均工资。这4个人的工资数值分别为$a$、 $b$、 $c$和$d$，和一个同态加密算法$E()$和其对应的解密算法$D()$。那么最终的平均值为$D(E(a)+E(b)+E(c)+E(d))/4$
  • 另外一个例子，有4个人分别知道且只知道一个数值，电商网站的流量，付费转化率，客单价和每月经营成本$a$、 $b$、$c$和$d$。那么最终电商网站的利润就是$D(E(a)\times E(b)\times E(c)-E(d))$

在公钥加密的早期，Rivest 指出了这种隐私计算的重要性，并称之为“隐私同态”。例如，RSA 加密允许进行乘法同态。

If $f(m)=m^2$ and we have access only to $c = E_d(m) = m^d \pmod{n}$, we can compute $c^2 \pmod{n}$ which is equal to the encryption of $m^2$

一个加密函数同时支持加法和乘法同态称为FHE函数。

FHE的步骤

  • 密钥生成
    • 生成公钥和私钥
    • 生成重线性化密钥：降低密文乘法导致增加的密文多项式次数
    • 生成旋转密钥：允许旋转/移动操作
  • 加密
    • 消息编码
    • 生成密文
  • 密文计算
    • 同态加法
    • 同态乘法
    • 噪声控制
    • 旋转
    • ……
  • 解密
    • 解密密文
    • 消息解码

FHE的计算

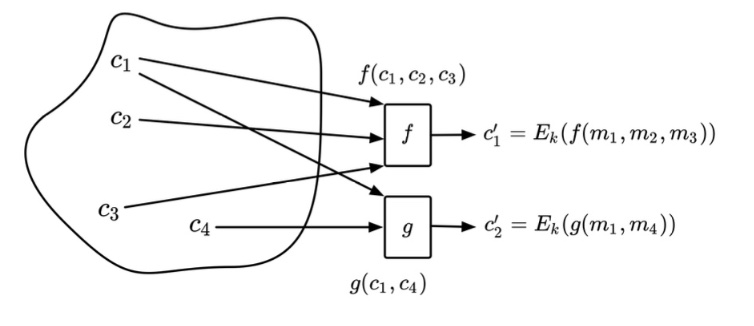
Fig. 1. FHE Computation

  • 明文$m_i$在相同的密钥下经过加密得到密文$c_i=E_k(m_i)$

  • 密文 $c_i$ 是函数 $ f $和 $g$的输入

  • 使用密文进行的算术运算称为同态计算，通常是密文的加法或乘法，或乘以一个标量值

  • 一个使用同态的计算机无法访问明文

  • 函数$f$和$g$的输出都是密文$c_1^{\prime}=f(c_1,c_2,c_3)$和$c_2^{\prime}=g(c_1,c_4)$

  • 解密$c_1^{\prime}$和$c_2^{\prime}$，得到

  • 这就是同态加密的“魔力”

  • 然而，事情并不像我描述的那么简单。要更好地理解FHE，需要更仔细地研究具体的FHE方法—它们之间存在很大差异

  • FHE方法在高效实现上面临巨大的挑战—密文的大小非常大

  • 将FHE提升到与公钥密码系统（PKC）相似的效率水平可能需要多年的集中研究

  • 在后续文章中，我将重点关注BFV算法和CKKS算法

  • BFV: Brakerski-Fan-Vercauteren

  • CKKS: Cheon-Kim-Kim-Song

客户端和服务器的计算

  • 客户端拥有密钥$k$ 和明文$m_i$

  • 客户端加密其数据$c_i = E_k(m_i)$

  • 客户端将密文$c_i$提供给服务器

  • 服务器只能访问密文$c_i$

  • 服务器进行同态加法$c_1 \oplus c_2$和同态乘法$c_3 \otimes c_4$。服务器将计算得到的密文$c_i^{\prime}$返回给客户端

  • 客户端解密密文$D_k(c_i^{\prime}) = m_i^{\prime}$，获得同态计算后的明文$m_i^{\prime}$

FHE的应用

FHE的应用非常广泛，被称为“密码学中的瑞士军刀”。

  • FHE允许在不泄漏隐私数据的情况下外包存储和计算。用户可以将隐私数据上传到云服务平台进行存储和计算

  • FHE允许对数据库进行私密查询；客户端可以在不让服务器知道检索到哪个记录的情况下获取数据记录

  • FHE还允许在不同的安全假设下进行两方计算和零知识协议的变体

FHE的限制

FHE的使用仍然存在一些限制。

  • 为了能够使用FHE进行计算，所有输入数据必须用相同的密钥加密

  • 由于FHE函数计算的输出是加密的，未经解密无法知道其正确的原始值

  • 尽管FHE能够对加密数据进行计算，但它无法检查输入是否经过正确加密，或计算是否按预期进行

FHE的历史发展　

FHE的概念实际上早在20世纪70年代末就已经被提出。1978年，密码学领域的几位研究者Rivest、Adleman和Dertouzos在他们的论文《On Data Banks and Privacy Homomorphisms》中首次提出了在密文上进行计算，从而间接操作原文的系统设想。后来，这一概念被重新总结并命名为全同态加密。

然而，人们并不能找到一个拥有全同态性质的完美算法，既能满足全同态所有条件，又能轻易证实其安全性的选项。

  • 第一代FHE系统：2009年，Craig Gentry在其博士论文中首次提出了一个合理且安全的FHE系统！这一系统基于理想格（ideal lattice）的假设。Gentry还提出了Bootstrapping的重要概念。Bootstrapping是一种针对密文的特殊处理技巧，通过这种处理可以将噪音接近临界值的密文“刷新”成噪音很低的新密文。通过Bootstrapping，一个有限级数系统的噪音可以永远不超过临界值，从而转变为全同态系统

  • 第二代FHE系统：2011年，两位研究者Brakerski和Vaikuntanathan提出了一种新的全同态加密体系，这一体系基于格（lattice）加密的另一种假设，即Learning with Errors（LWE），代表性的有BFV方案和BGV方案。这一类体系主要以有限级数的同态加密系统为主，但可以通过Bootstrapping的方式转变为全同态系统。与Gentry在2009年提出的系统相比，该体系使用了更实际的LWE假设

  • 第三代FHE系统：2013年，Gentry、Sahai和Waters共同提出了新的GSW全同态加密系统。GSW系统与BGV系统相似，具有有限级数全同态性质，基于更为简单的LWE假设，并且通过Bootstrapping可以达到全同态。此后，在原来的三代全同态系统基础之上，出现了各种各样新的设计，致力于优化和加速BGV与GSW系统的运行效率，比较著名的方案有FHEW和TFHE等

  • 第四代FHE系统：2017年，Cheon、Kim、Kim和Song推出了近似同态加密CKKS算法，其具体构造基于BGV方案，但也可以依赖于其他现有的同态加密方案。不同于以往同态加密算法中所追求的解密结果和明文完全一致，CKKS算法的目标是进行近似计算。这并不会偏离需求，因为现实生活中大部分运算面对的是实数（或复数），而实数（或复数）的运算往往只需要保留一部分有效数字即可。此外，相比于其他基于LWE/RLWE难题的同态方案，CKKS允许误差并放宽准确性的限制，这简化了细节并大大提升了计算效率。CKKS方案被广泛应用在隐私保护机器学习等场景中

FHE的库

现阶段已经有非常多成熟的全同态加密库，主要包含cuFHE、FHEW、FV-NFLib、HEAAN、HElib、PALISADE、SEAL、TFHE 和 Lattigo。

库/方案 FHEW TFHE BGV BFV CKKS
cuFHE ✅
FHEW ✅
Pyfhel ✅ ✅ ✅
HEAAN ✅
Helib ✅ ✅
PALISADE ✅ ✅ ✅
SEAL ✅ ✅
TFHE ✅ ✅ ✅ ✅
Lattigo ✅ ✅ ✅

除了开发传统的全同态库之外，还有许多团队在研究如何通过GPU、FPGA、ASIC等异构硬件来更好地加速全同态加密算法的计算。比如，cuFHE就是一个比较有名的基于CUDA的GPU加速全同态加密系统。

-------------　　　　本文结束　　感谢阅读　　　　-------------